Rabidgremlin's
Soapbox

As this slightly over the top presentation shows adding motion, bounce and wiggle to your game elements can really make a game feel rich and alive:

Luckily this is easy to achieve with the GoKit tweening library that is included with Futile. The library allows you to easily change any property of an object over a specific period of time.

For instance this bit of code:

skyline.scaleY =0.1f;
Go.to(skyline, 0.75f, new TweenConfig ().     
      floatProp("scaleY", 1.0f).
      setEaseType(EaseType.BounceOut));

Sets the skyline sprite’s y scale to 0.1, it then uses the GoKit tweening library to scale the skyline sprite’s Y scale back to 1 over a period of 750ms with an ease of  BounceOut.

The effect of this is have the skyline spring out of the ground with a nice cartoony bounce. Adding some tweens to the title screen’s sprites like this:

private void AnimateIntro()
{
    bg.y = Futile.screen.height+70;
    bg.rotation = 10f;

    Go.to(bg, 0.5f, new TweenConfig ().
        setDelay(0.5f).
        floatProp("y", 0f).
        floatProp("rotation", 0f).
        setEaseType(EaseType.BounceOut));

    skyline.scaleY =0.1f;
    Go.to(skyline, 0.75f, new TweenConfig ().
        setDelay(1.0f).
        floatProp("scaleY", 1.0f).
        setEaseType(EaseType.BounceOut));

    title.scale = 0.001f;
    Go.to(title, 0.3f, new TweenConfig ().
        setDelay(1.5f).         
        floatProp("scale", 1.0f).
        setEaseType(EaseType.SineOut));

    nuke.scaleY = 0.001f;
    Go.to(nuke, 0.5f, new TweenConfig ().
        setDelay(2.3f).         
        floatProp("scaleY", 1.0f).
        setEaseType(EaseType.BounceOut));

    startButton.scaleY = 0.0f;

    Go.to(startButton, 0.5f, new TweenConfig ().
        setDelay(3.2f).
        floatProp("scaleY", 1.0f).
        setEaseType(EaseType.BounceOut));

    helpButton.scaleY = 0.0f;

    Go.to(helpButton, 0.5f, new TweenConfig ().
        setDelay(3.3f).
        floatProp("scaleY", 1.0f).
        setEaseType(EaseType.BounceOut));
}

Along with a tween to make the buttons disappear when we tap them on the game screen, gets us this:

So how exactly do these tweens work? Well it’s all down to some clever maths. The GoKit library implements what are known as the Robert Penner equations which are a set of equations that he published in a book called Programming Macromedia Flash MX. These equations can be used to produce organic feeling motions and change.

Basically these equations all take the form of a function that takes 4 parameters:

• t – current time unit
• b – the starting value
• c – the total change of the value over the duration
• d – the duration

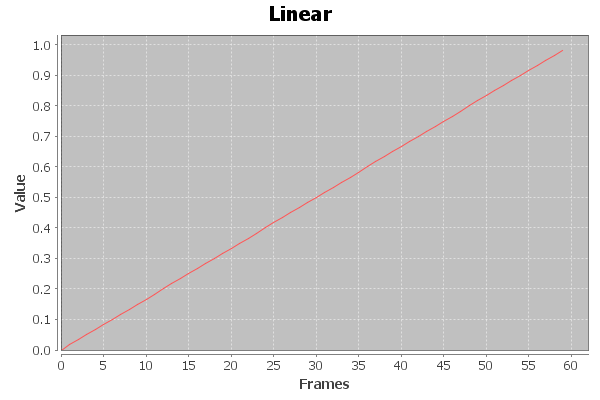
The simplest of these doesn’t in fact result in any easing, it simply creates a linear motion:

public float EaseNone( float t, float b, float c, float d )
{
    return c * t / d + b;
}

Plotting this out on graph gives us this (with a starting point of 0, a change of 1, over 60 frames):

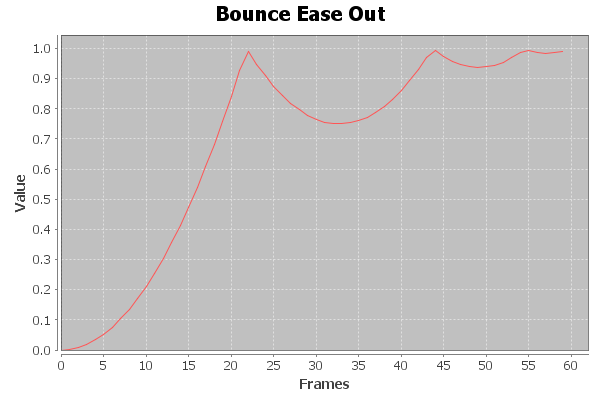
The bounce out equation is a bit more interesting:

public float EaseOut(float t, float b, float c, float d)
{
    if ((t /= d) < (1 / 2.75))
    {
      return c * (7.5625f * t * t) + b;
    }
    else if (t < (2 / 2.75))
    {
      return c * (7.5625f * (t -= (1.5f / 2.75f)) * t + .75f) + b;
    }
    else if (t < (2.5 / 2.75))
    {
      return c * (7.5625f * (t -= (2.25f / 2.75f)) * t + .9375f) + b;
    }
    else
    {
      return c * (7.5625f * (t -= (2.625f / 2.75f)) * t + .984375f) + b;
    }
}

Plotting this out looks like this:

Which is a much more interesting motion.

All in all there are 31 different eases in the library. This chart shows them all:

Next up I’m going to kick things up a notch and get the basic game play in place.